---

  蓝桥杯个人赛软件类历届真题及其解析

---

试题 A: 合数个数

本题总分：$5$ 分

---

【问题描述】

  一个数如果除了 $1$ 和自己还有其他约数，则称为一个合数。例如：$1,2,3$ 不是合数，$4,6$ 是合数。

  请问从 $1$ 到 $2020$ 一共有多少个合数。

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1713

---

#include <stdio.h>

const int N = 2020;

int ans, factor[N + 1];

int main() {
    for (int i = 2; i <= N; ++i)
        if (factor[i]) ++ans;
        else
            for (int j = i; j <= N; j += i)
                factor[j] = 1;
    printf("%d", ans);
}

  这码风，程序设计老师看了直摇头。

---

试题 B: 含 2 天数

本题总分：$5$ 分

---

【问题描述】

  小蓝特别喜欢 $2$，今年是公元 $2020$ 年，他特别高兴，因为每天日历上都可以看到 2。

  如果日历中只显示年月日，请问从公元 $1900$ 年 $1$ 月 $1$ 日到公元 $9999$ 年 $12$ 月 $31$ 日，一共有多少天日历上包含 $2$。即有多少天中年月日的数位中包含数字 $2$。

---

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1994240

---

#include <stdio.h>

int ans, days[]{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int isLeap(int year) { return !(year % 100 ? year % 4 : year % 400); }

int contain2(int num) { do if (num % 10 == 2) return 1; while (num /= 10); }

int main() {
    for (int year = 1900; year <= 9999; ++year) {
        if (isLeap(year)) days[2] = 29;
        for (int month = 1; month <= 12; ++month)
            for (int day = 1; day <= days[month]; ++day)
                if (contain2(year) || contain2(month) || contain2(day)) ++ ans;
        days[2] = 28;
    }
    printf("%d", ans);
}

  摇头。

---

试题 C: 本质上升序列

本题总分：$10$ 分

---

【问题描述】

  小蓝特别喜欢单调递增的事物。

  在一个字符串中，如果取出若干个字符，将这些字符按照在字符串中的顺序排列后是单调递增的，则成为这个字符串中的一个单调递增子序列。

  例如，在字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$ 中，如果取出字符 $\mathrm{n}$ 和 $\mathrm{q}$，则 $\mathrm{n}\mathrm{q}$ 组成一个单调递增子序列。类似的单调递增子序列还有 $\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{i}$、$\mathrm{a}\mathrm{n}\mathrm{o}$ 等等。

  小蓝发现，有些子序列虽然位置不同，但是字符序列是一样的，例如取第二个字符和最后一个字符可以取到 $\mathrm{a}\mathrm{o}$，取最后两个字符也可以取到 $\mathrm{a}\mathrm{o}$。
  小蓝认为他们并没有本质不同。

  对于一个字符串，小蓝想知道，本质不同的递增子序列有多少个？

  例如，对于字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$，本质不同的递增子序列有 $21$ 个。它们分别是 $\mathrm{l}$、$\mathrm{a}$、$\mathrm{n}$、$\mathrm{q}$、$\mathrm{i}$、$\mathrm{o}$、$\mathrm{l}\mathrm{n}$、$\mathrm{a}\mathrm{n}$、$\mathrm{l}\mathrm{q}$、$\mathrm{a}\mathrm{q}$、$\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{i}$、$\mathrm{l}\mathrm{o}$、$\mathrm{a}\mathrm{o}$、$\mathrm{n}\mathrm{o}$、$\mathrm{i}\mathrm{o}$、$\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{n}\mathrm{q}$、$\mathrm{l}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{i}\mathrm{o}$。

  请问对于以下字符串（共 $200$ 个小写英文字母，分四行显示）：（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt，内容与下面的文本相同）

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

  本质不同的递增子序列有多少个？

---

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

3616159

---

动态规划

---

  首先考虑上升子序列问题，即子串可以相同的情况。

  设 $f_i$ 为以字符串 $S[1,n]$ 第 $i$ 个字符结尾的最长递增子序列的个数，则总个数为 ${\sum }_{i=1}^n{f}_i$，状态转移方程为 $f_i={\sum }_{j=1}^{i-1}{f}_j(S[i]>S[j])$。

  为了避免出现重复子串，考虑互斥的划分方式，

  有状态 $f_{i,c}$ 表示到第 $i$ 个字符为止，以 $c$ 结尾的本质不同子串的个数为多少，显然答案为 ${\sum }_c{f}_{n,c}$。

  可是如何保证不重不漏呢？

  对于 $c\ne S[i]$，显然有 $f_{i,c}=f_{i-1,c}$，而对于 $c=S[i]$ 的情况，考虑重新统计即 $f_{i,c}={\sum }_{c^{\prime }=1}^{c-1}{f}_{i-1,c^{\prime }}$，不重是做到了，即可不重不漏。

   证明半天证明了一坨屎，其实可以用反证法，但反证太无聊了。

#include <iostream>

std::string s = "$", buf;

int dp[0xff], ans;

int main() {
    freopen("inc.txt", "r", stdin);
    while (std::cin >> buf) s += buf;
    for (int i = 1; i <= 200; ++i) {
        ans -= dp[s[i]], dp[s[i]] = 1;
        for (int j = s[i] - 1; j >= 'a'; --j) dp[s[i]] += dp[j];
        ans += dp[s[i]];
    }
    printf("%d", ans);
}

---

试题 D: 咫尺天涯

本题总分：$10$ 分

---

【问题描述】

  皮亚诺曲线是一条平面内的曲线。

  下图给出了皮亚诺曲线的 $1$ 阶情形，它是从左下角出发，经过一个 $3\times 3$ 的方格中的每一个格子，最终到达右上角的一条曲线。

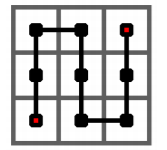
  设每个格子的边长为 $1$，在上图中，有的相邻的方格（四相邻）在皮亚诺曲线中也是相邻的，在皮亚诺曲线上的距离是 $1$，有的相邻的方格在皮亚诺曲线中不相邻，距离大于 $1$。

  例如，正中间方格的上下两格都与它在皮亚诺曲线上相邻，距离为 $1$，左右两格都与它在皮亚诺曲线上不相邻，距离为 $3$。

  下图给出了皮亚诺曲线的 $2$ 阶情形，它是经过一个 $3^2\times 3^2$ 的方格中的每一个格子的一条曲线。它是将 $1$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

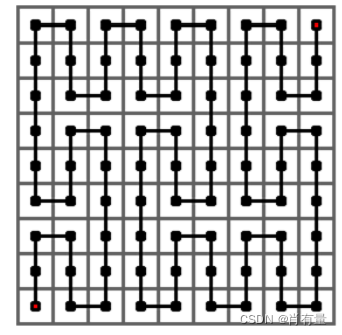
  下图给出了皮亚诺曲线的 $3$ 阶情形，它是经过一个 $3^3\times 3^3$ 的方格中的每一个格子的一条曲线。它是将 $2$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

  皮亚诺曲线总是从左下角开始出发，最终到达右上角。

  小蓝对于相邻的方格在皮亚诺曲线上的相邻关系很好奇，他想知道相邻的方格在曲线上的距离之和是多少。

  例如，对于 $1$ 阶皮亚诺曲线，距离和是 $24$，有 $8$ 对相邻的方格距离为 $1$，$2$ 对相邻的方格距离为 $3$，$2$ 对相邻的方格距离为 $5$。

  再如，对于 $2$ 阶皮亚诺曲线，距离和是 $816$。

  请求出对于 $12$ 阶皮亚诺曲线，距离和是多少。

  提示：答案不超过 $10^{18}$。

---

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

184731576397539360

---

动态规划

---

  首先考虑分形问题，但是 $3^{12}\times 3^{12}$ 的曲线中，相邻的格子对有 $2\times 3^{12}\times (3^{12}-1)$ 个，复杂度爆炸。

  于是考虑动态规划，为此需要选择一些合适的属性来表述状态，合适的策略来完成转移。

  容易想到按阶划分，即将一个 $k$ 阶的皮亚诺曲线划分为 $3^3$ 个 $k-1$ 的皮亚诺曲线，而 $k-1$ 阶曲线内部相邻块的距离不受其余同阶曲线的影响，固有状态 $f_i$ 表示 $i$ 阶皮亚诺曲线的距离合，$f_i=3^3{f}_{i-1}+I_i$，$I_i$ 表示 $k-1$ 阶曲线直接相邻部分的距离合，而这正是下面要着重讨论的部分。

  对于 $2$ 阶皮亚诺曲线，它的 $1$ 阶曲线相邻的块有：

  容易发现，两行或两列之间相邻块的距离是相等的，于是只需讨论出一行一列的距离合的计算方法，将其和乘以 $2$ 即可计算出 $I_2$。

  其实到这一步问题已经得解，因为分形去求解两块之间的距离， $O(3^n)$ 的复杂度完全可以在短时间内计算出结果。

#include <stdio.h>

typedef long long ll;

ll ans, tmp, pow[14]{0, 1};

ll abs(ll a) { return a > 0 ? a : -a; }

ll calc(int k, ll x, ll y) {
    if (k == 0) return 0;
    ll offset = x / pow[k] * 3;
    int flag = offset == 3;
    offset += flag ? (3 - y / pow[k] - 1) : (y / pow[k]);
    if ((offset & 1) == 1)
        x =  pow[k] - x % pow[k] - 1;
    return flag ? ((offset + 1) * pow[k] * pow[k] - calc(k - 1, x % pow[k], y % pow[k]) - 1) :
           (offset * pow[k] * pow[k] + calc(k - 1, x % pow[k], y % pow[k])) ;
}

int main() {
    for (int i = 2; i <= 13; i++) pow[i] = pow[i - 1] * 3;
    for (int i = 1; i <= 12; i++) {
        tmp = 0;
        for (int j = 0; j < pow[i + 1]; j++) {
            tmp += abs(calc(i, j, pow[i]) - calc(i, j, pow[i] - 1));
            tmp += abs(calc(i, pow[i], j) - calc(i, pow[i] - 1, j));
        }
        ans = 9 * ans + 2 * tmp;
    }
    printf("%lld", ans);
}

  有关 分形问题。

---

试题 E: 玩具蛇

本题总分：$15$ 分

---

【问题描述】

  小蓝有一条玩具蛇，一共有 $16$ 节，上面标着数字 $1$ 至 $16$。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。

  小蓝还有一个 $4\times 4$ 的方格盒子，用于存放玩具蛇，盒子的方格上依次标着字母 $\mathrm{A}$ 到 $\mathrm{P}$ 共 $16$ 个字母。

  小蓝可以折叠自己的玩具蛇放到盒子里面。他发现，有很多种方案可以将玩具蛇放进去。

  下图给出了两种方案：

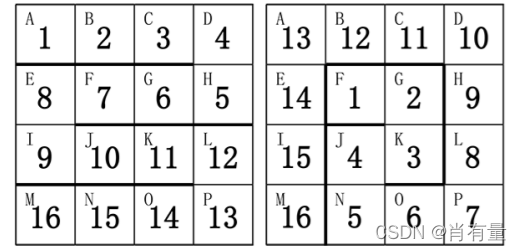
  请帮小蓝计算一下，总共有多少种不同的方案。如果两个方案中，存在玩具蛇的某一节放在了盒子的不同格子里，则认为是不同的方案。

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

552

---

深度优先搜索

---

  模板题。

#include <stdio.h>

const int N = 4, M = 4, target = N * M;

int ans, visited[N + 2][M + 2], offset[4][2]{-1, 0, 0, 1, 1, 0, 0, -1};

void dfs(int x, int y, int depth) {
    visited[x][y] = 1;
    if (depth == target) ++ans;
    for (int i = 0; i < 4; ++i)
        if (!visited[x + offset[i][0]][y + offset[i][1]])
            dfs(x + offset[i][0], y + offset[i][1], depth + 1);
    visited[x][y] = 0;
}

int main() {
   for (int i = 1; i <= N; ++i) visited[i][0] = visited[i][M + 1] = 1;
   for (int i = 1; i <= M; ++i) visited[0][i] = visited[N + 1][i] = 1;
   for (int i = 1; i <= N; ++i)
       for (int j = 1; j <= M; ++j) dfs(i, j, 1);
   printf("%d", ans);
}

---

试题 F: 皮亚诺曲线距离

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$15$ 分

---

【问题描述】

  皮亚诺曲线是一条平面内的曲线。

  下图给出了皮亚诺曲线的 $1$ 阶情形，它是从左下角出发，经过一个 $3\times 3$ 的方格中的每一个格子，最终到达右上角的一条曲线。

  下图给出了皮亚诺曲线的 $2$ 阶情形，它是经过一个 $3^2\times 3^2$ 的方格中的每一个格子的一条曲线。它是将 $1$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

  下图给出了皮亚诺曲线的 $3$ 阶情形，它是经过一个 $3^3\times 3^3$ 的方格中的每一个格子的一条曲线。它是将 $2$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

  皮亚诺曲线总是从左下角开始出发，最终到达右上角。

  我们将这些格子放到坐标系中，对于 k 阶皮亚诺曲线，左下角的坐标是 ($0$, $0$)，右上角坐标是 ($3^k-1$, $3^k-1$)，右下角坐标是 ($3^k-1$, $0$)，左上角坐标是($0$, $3^k-1$)。

  给定 k 阶皮亚诺曲线上的两个点的坐标，请问这两个点之间，如果沿着皮亚诺曲线走，距离是到少？

【输入格式】

  输入的第一行包含一个正整数 $k$，皮亚诺曲线的阶数。

  第二行包含两个整数 $x_1$, $y_1$，表示第一个点的坐标。

  第三行包含两个整数 $x_2$, $y_2$，表示第二个点的坐标。

【输出格式】

  输出一个整数，表示给定的两个点之间的距离。

【样例输入 1】

1
0 0
2 2

【样例输出 1】

8

【样例输入 2】

2
0 2
0 3

【样例输出 2】

13

【评测用例规模与约定】

  对于 $30\%$ 的评测用例，$0\le k\le 10$。
  对于 $50\%$ 的评测用例，$0\le k\le 20$。
  对于所有评测用例，$0\le k\le 100,0\le x_1,y_1,x_2,y_2<3^k,x_1,y_1,x_2,y_2\le 10^{18}$。数据保证答案不超过 $10^{18}$。

---

分形问题

---

  如 $\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}$ 这种，以一定规律无限包含自身的图，可以被称为分形图。

  其衍生出的问题，自然是分形问题。

  我们设 $calc(x,y)=(0,0)$ 到 $(x,y)$ 的距离，

  显然答案等于 $abs(calc(x_1,y_1)-calc(x_2,y_2))$。

  不难看出，一个 $k+1$ 阶皮亚诺曲线由 $2$ 种 $k$ 阶皮亚诺曲线连接构成，$k>0$。

  相信大 伙看到这个图就已经知道程序怎么实现了，过。

  其中一种 $k$ 阶皮亚诺曲线为另一种的水平翻转，即 $y$ 轴坐标取反，而中线这段皮亚诺曲线与其他曲线的区别在于起点与终点相反，我可以计算出其中一种，再用曲线的大小减去它。

  综上我们可以选择一个策略，

  先按离原点的距离将 $k$ 阶皮亚诺曲线分成 $0\sim 8$ 块 $k-1$ 阶曲线，显然在这个意义上 $k-1$ 阶曲线与 $k-1$ 阶曲线的水平翻转交替出现，如果坐标落在 $k-1$ 阶曲线的水平翻转上，$y$ 取其模 $3^{k-1}$ 的补数。

  再递归计算坐标所在的 $k-1$ 曲线离其原点的距离，如果坐标落在中线上则用 $k-1$ 阶曲线的长度减去递归计算到的距离，最后加上编号乘以 $k-1$ 阶曲线的长度，

  就得到了一个点到原点的距离。

  为了避免爆long long，无论 $k$ 为多少，我们都至多视其为 $38$，因为 $3^{38}>10^{18}$，而 $x,y$ 不会大于 $10^{18}$，故而无论$k$大于 $38$多少，我们都将其视为左下角第一个 $38$ 阶 $\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}$ 即可，但即使这样依然可能会爆 long long，故我们选用__int128。

---

  这里提一下关于网络上，在蓝桥杯时使用__int128无法通过编译的论调。

  截止至 $2022$ 年 $5$ 月 $5$ 日 $23:35:40$，

  “蓝桥杯”练习系统 在 系统介绍 第六条提到：

  6. 比赛环境：使用和软件大赛相同的测试环境进行测试，有效的模拟大赛的评测。

  然后在 编译环境 提到 $\mathrm{C}/\mathrm{C}$++ 的编译环境：

  $\mathrm{C}$：    gcc (GCC) 4.9.2

  $\mathrm{C}$++：g++ (GCC) 4.9.2

  而在 GCC 4.6 Release Series 中我们能看到：

  C family

  Support for a new data type __int128 for targets having wide enough machine-mode support.

  爱用不用，反正我用。

---

#include <stdio.h>

int block[3][3]{0, 1, 2, 5, 4, 3, 6, 7, 8};

long long x1, y1, x2, y2, pow[38] = {0, 1};

__int128 calc(int k, long long x, long long y) {
    if (k == 0) return 0;
    __int128 res = block[x / pow[k]][y / pow[k]];
    if (res & 1) x = pow[k] - x % pow[k] - 1;
    return res / 3 != 1 ?
        res * pow[k] * pow[k] + calc(k - 1, x % pow[k], y % pow[k]) :
        (res + 1) * pow[k] * pow[k] - calc(k - 1, x % pow[k], y % pow[k]) - 1;
}

long long abs(long long a) { return a > 0 ? a : -a; }

int min(int a, int b) { return a < b ? a : b; }

int k;

int main() {
    scanf("%d %lld %lld %lld %lld", &k, &x1, &y1, &x2, &y2);
    for (int i = 2; i <= 38; ++i) pow[i] = 3 * pow[i - 1];
    printf("%lld", abs(calc(min(k, 38), x1, y1) - calc(min(k, 38), x2, y2)));
}

---

试题 G: 出租车

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

【问题描述】

  小蓝在 $L$ 市开出租车。

  $L$ 市的规划很规整，所有的路都是正东西向或者正南北向的，道路都可以看成直线段。东西向的道路互相平行，南北向的道路互相平行，任何一条东西向道路垂直于任何一条南北向道路。

  从北到南一共有 $n$ 条东西向道路，依次标号为 $H_1,H_2,\cdots ,H_n$。从西到东一共有 $m$ 条南北向的道路，依次标号为 $S_1,S_2,\cdots ,S_m$。

  每条道路都有足够长，每一条东西向道路和每一条南北向道路都相交，$H_i$ 与 $S_j$ 的交叉路口记为 $(i,j)$。

  从 $H_1$ 和 $S_1$ 的交叉路口 $(1,1)$ 开始，向南遇到的路口与 $(1,1)$ 的距离分别是 $h_1,h_2,\cdots ,h_{n-1}$，向东遇到路口与 $(1,1)$ 的距离分别是 $w_1,w_2,\cdots ,w_{m-1}$。

  道路的每个路口都有一个红绿灯。

  时刻 $0$ 的时候，南北向绿灯亮，东西向红灯亮，南北向的绿灯会持续一段时间（每个路口不同），然后南北向变成红灯，东西向变成绿灯，持续一段时间后，再变成南北向绿灯，东西向红灯。

  已知路口 $(i,j)$ 的南北向绿灯每次持续的时间为 $g_{ij}$，东西向的绿灯每次持续的时间为 $r_{ij}$，红绿灯的变换时间忽略。

  当一辆车走到路口时，如果是绿灯，可以直行、左转或右转。如果是红灯，可以右转，不能直行或左转。如果到路口的时候刚好由红灯变为绿灯，则视为看到绿灯，如果刚好由绿灯变为红灯，则视为看到红灯。

  每段道路都是双向道路，道路中间有隔离栏杆，在道路中间不能掉头，只能在红绿灯路口掉头。掉头时不管是红灯还是绿灯都可以直接掉头。掉头的时间可以忽略。

  小蓝时刻 $0$ 从家出发。今天，他接到了 $q$ 个预约的订单，他打算按照订单的顺序依次完成这些订单，就回家休息。中途小蓝不准备再拉其他乘客。

  小蓝的家在两个路口的中点，小蓝喜欢用 $x_1,y_1,x_2,y_2$ 来表示自己家的位置，即路口 $(x_1,y_1)$ 到路口 $(x_2,y_2)$ 之间的道路中点的右侧，保证两个路口相邻（中间没有其他路口）。请注意当两个路口交换位置时，表达的是路的不同两边，路中间有栏杆，因此这两个位置实际要走比较远才能到达。

  小蓝的订单也是从某两个路口间的中点出发，到某两个路口间的中点结束。小蓝必须按照给定的顺序处理订单，而且一个时刻只能处理一个订单，不能图省时间而同时接两位乘客，也不能插队完成后面的订单。

  小蓝只对 $L$ 市比较熟，因此他只会在给定的 $n$ 条东西向道路和 $m$ 条南北向道路上行驶，而且不会驶出 $H_1,H_n,S_1,S_m$ 这几条道路所确定的矩形区域（可以到边界）。

  小蓝行车速度一直为 $1$，乘客上下车的时间忽略不计。

  请问，小蓝最早什么时候能完成所有订单回到家。

【输入格式】

  输入第一行包含两个整数 $n,m$，表示东西向道路的数量和南北向道路的数量。

  第二行包含 $n-1$ 个整数 $h_1,h_2,\cdots ,h_{n-1}$。

  第三行包含 $m-1$ 个整数 $w_1,w_2,\cdots ,w_{m-1}$。

  接下来 $n$ 行，每行 $m$ 个整数，描述每个路口南北向绿灯的时间，其中的第 $i$ 行第 $j$ 列表示 $g_{ij}$。

  接下来 $n$ 行，每行 $m$ 个整数，描述每个路口东西向绿灯的时间，其中的第 $i$ 行第 $j$ 列表示 $r_{ij}$。

  接下来一行包含四个整数 $x_1,y_1,x_2,y_2$，表示小蓝家的位置在路口 $(x_1,y_1)$ 到路口 $(x_2,y_2)$ 之间的道路中点的右侧。

  接下来一行包含一个整数 $q$，表示订单数量。

  接下来 $q$ 行，每行描述一个订单，其中第 $i$ 行包含八个整数 $x_{i1},y_{i1},x_{i2},y_{i2},x_{i3},y_{i3},x_{i4},y_{i4}$，表示第 $i$ 个订单的起点为路口 $(x_{i1},y_{i1})$ 到路口 $(x_{i2},y_{i2})$ 之间的道路中点的右侧，第 $i$ 个订单的终点为路口 $(x_{i3},y_{i3})$ 到路口 $(x_{i4},y_{i4})$ 之间的道路中点的右侧。

【输出格式】

  输出一个实数，表示小蓝完成所有订单最后回到家的最早时刻。四舍五入保留一位小数。

【样例输入】

2 3
200
100 400
10 20 10
20 40 30
20 20 20
20 20 20
2 1 1 1
1
2 2 1 2 1 2 1 3

【样例输出】

1620.0

【样例说明】
  小蓝有一个订单，他的行车路线如下图所示。其中 $H$ 表示他家的位置，$S$ 表示订单的起点，$T$ 表示订单的终点。小明在最后回家时要在直行的红绿灯路口等绿灯，等待时间为 $20$。

【评测用例规模与约定】

  对于 $20\%$ 的评测用例，$1\le n,m\le 5，1\le q\le 10$。
  对于 $50\%$ 的评测用例，$1\le n,m\le 30，1\le q\le 30$。
  对于所有评测用例，$1\le n,m\le 100，1\le q\le 30，1\le h_1<h_2<\cdots <h_{n-1}\le 100000，1\le w_1<w_2<\cdots <w_{m-1}\le 100000，1\le g_{ij}\le 1000，1\le r_{ij}\le 1000$，给定的路口一定合法。

---

// 大模拟，没有写的意义。

---

试题 H: 答疑

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

【问题描述】

  有 $n$ 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。

  老师可以安排答疑的顺序，同学们要依次进入老师办公室答疑。

  一位同学答疑的过程如下：

  1. 首先进入办公室，编号为 $i$ 的同学需要 $s_i$ 毫秒的时间。

  2. 然后同学问问题老师解答，编号为 $i$ 的同学需要 $a_i$ 毫秒的时间。

  3. 答疑完成后，同学很高兴，会在课程群里面发一条消息，需要的时间可以忽略。

  4. 最后同学收拾东西离开办公室，需要 $e_i$ 毫秒的时间。一般需要 $10$ 秒、$20$ 秒或 $30$ 秒，即 $e_i$ 取值为 $10000$，$20000$ 或 $30000$。

  一位同学离开办公室后，紧接着下一位同学就可以进入办公室了。

  答疑从 $0$ 时刻开始。老师想合理的安排答疑的顺序，使得同学们在课程群里面发消息的时刻之和最小。

【输入格式】

  输入第一行包含一个整数 $n$，表示同学的数量。

  接下来 $n$ 行，描述每位同学的时间。其中第 $i$ 行包含三个整数 $s_i$, $a_i$, $e_i$，意义如上所述。

【输出格式】

  输出一个整数，表示同学们在课程群里面发消息的时刻之和最小是多少。

【样例输入】

3
10000 10000 10000
20000 50000 20000
30000 20000 30000

【样例输出】

280000

【样例说明】
  按照 $1,3,2$ 的顺序答疑，发消息的时间分别是 $20000,80000,180000$。

【评测用例规模与约定】

  对于 $30\%$ 的评测用例，$1\le n\le 20$。
  对于 $60\%$ 的评测用例，$1\le n\le 200$。
  对于所有评测用例，$1\le n\le 1000$，$1\le s_i\le 60000$，$1\le a_i\le 1000000$， e i ∈ { 10000 , 20000 , 30000 } e_i\in\{10000,20000,30000\} ei​∈{10000,20000,30000}，即 $e_i$ 一定是 $10000、20000、30000$ 之一。

---

贪心

---

  第 $i$ 个同学在第 $i^{\prime }$ 位被答疑，在课程群里面发消息的时刻为：

  $\sum _{j^{\prime }=1}^{i^{\prime }}(s_{j^{\prime }}+a_{j^{\prime }}+e_{j^{\prime }})-e_{i^{\prime }}$

  故同学们在课程群里面发消息的时刻之和为：

  $\sum _{i^{\prime }=1}^n\sum _{j^{\prime }=1}^{i^{\prime }}(s_{j^{\prime }}+a_{j^{\prime }}+e_{j^{\prime }})-\sum _{i^{\prime }=1}^n{e}_{i^{\prime }}$

  设 $B_i=s_i+a_i+e_i$，考虑答疑顺序按 $B_i$ 降序排序，可以发现对于任意 $i^{\prime },j^{\prime }$，$B_i\ne B_j$，交换都会使答案增加 $(j^{\prime }-i^{\prime })(B_j-B_i)$，故上述次序是一个最优解。

#include <stdio.h>
#include <algorithm>

int n, s, a, e, B[1001];

long long ans, sum;

bool cmp(int a, int b) { return a > b; }

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d %d %d", &s, &a, &e),
        ans -= e, B[i] = s + a + e;
    std::sort(B + 1, B + n + 1, cmp);
    for (int i = 1; i <= n; ++i)
        sum += B[i], ans += i * B[i];
    printf("%lld", ans);
}

---

试题  I: 奇偶覆盖

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

【问题描述】

  在平面内有一些矩形，它们的两条边都平行于坐标轴。

  我们称一个点被某个矩形覆盖，是指这个点在矩形的内部或者边界上。

  请问，被奇数个矩形覆盖和被偶数 $(\ge 2)$ 个矩形覆盖的点的面积分别是多少？

【输入格式】

  输入的第一行包含一个整数 $n$，表示矩形的个数。

  接下来 $n$ 行描述这些矩形，其中第 $i$ 行包含四个整数 $l_i,b_i,r_i,t_i$ ，表示矩形的两个对角坐标分别为 $(l_i,b_i),(r_i,t_i)$。

【输出格式】

  输出两行。
  第一行包含一个整数，表示被奇数个矩形覆盖的点的面积。
  第二行包含一个整数，表示被偶数 $(\ge 2)$ 个矩形覆盖的点的面积。

【样例输入】

3
1 1 3 3
2 2 4 4
3 3 5 5

【样例输出】

8
2

【评测用例规模与约定】

  对于 $20$% 的评测用例，$1\le n\le 10,0\le l_i<r_i\le 100,0\le b_i<t_i\le 100$。
  对于 $40$% 的评测用例，$1\le n\le 1000,0\le l_i<r_i\le 100,0\le b_i<t_i\le 100$。
  对于 $60$% 的评测用例，$1\le n\le 10000,0\le l_i<r_i\le 1000,0\le b_i<t_i\le 1000$。
  对于 $80$% 的评测用例，$1\le n\le 100000,0\le l_i<r_i\le 100000,0\le b_i<t_i\le 100000$。
  对于所有评测用例，$1\le n\le 100000,0\le l_i<r_i\le 10^9,0\le b_i<t_i\le 10^9$。

---

扫描线

---

  写完就后悔了，一般扫描线有两种写法，一种是将子区间二进制拆分建线段树，在这道题里最少要开 $n$ 的 $8$ 倍内存，另一种则是端点表示法，$[l,r]$ 表示 $[l,r+1]$ 间的信息，在这道题里值要开 $n$ 的 $4$ 倍内存，

  但我写都写了，过，下一道。

#include <stdio.h>
#include <algorithm>

const int N = 100009;

long long oddc, evenc;

int S[N << 1], L[N << 4], R[N << 4], length[N << 4], odd[N << 4], even[N << 4], cover[N << 4];

void build(int rt, int l, int r) {
    L[rt] = S[l], R[rt] = S[r], length[rt] = S[r] - S[l];
    if (r - l > 1) {
        build(rt << 1, l, l + r >> 1);
        build(rt << 1 | 1, l + r >> 1, r);
    }
}

void push_up(int rt) {
    odd[rt] = odd[rt << 1] + odd[rt << 1 | 1];
    even[rt] = even[rt << 1] + even[rt << 1 | 1];
    if (cover[rt])
        if (cover[rt] & 1)
            std::swap(odd[rt], even[rt]), odd[rt] = length[rt] - even[rt];
        else
            even[rt] = length[rt] - odd[rt];
}

void update(int rt, int l, int r, int k) {
    if (l >= r) return;
    if (L[rt] == l && R[rt] == r) cover[rt] += k;
    else {
        if (l <= R[rt << 1])
            update(rt << 1, l, std::min(r, R[rt << 1]), k);
        if (r >= L[rt << 1 | 1])
            update(rt << 1 | 1, std::max(l, L[rt << 1 | 1]), r, k);
    }
    push_up(rt);
}

struct line {
    int x1, x2, y, flag;
    inline bool operator<(const line &l) const { return y < l.y; }
} lines[N << 1];

int n, l, b, r, t;

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d %d %d %d", &l, &b, &r, &t);
        lines[i] = {l, r, b,  1};
        lines[i + n] = {l, r, t, -1};
        S[i] = l, S[i + n] = r;
    }
    std::sort(S, S + 2 * n);
    std::sort(lines, lines + 2 * n);
    build(1, 0, std::unique(S, S + 2 * n) - S - 1);
    update(1, lines->x1, lines->x2, 1);
    for (int i = 1; i < 2 * n; ++i) {
        oddc += (long long)(lines[i].y - lines[i - 1].y) * odd[1];
        evenc += (long long)(lines[i].y - lines[i - 1].y) * even[1];
        update(1, lines[i].x1, lines[i].x2, lines[i].flag);
    }
    printf("%lld\n%lld", oddc, evenc);
}

---

试题 J: 蓝跳跳

时间限制: $2.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

【问题描述】

  小蓝制作了一个机器人，取名为蓝跳跳，因为这个机器人走路的时候基本靠跳跃。

  蓝跳跳可以跳着走，也可以掉头。蓝跳跳每步跳的距离都必须是整数，每步可以跳不超过 $k$ 的长度。由于蓝跳跳的平衡性设计得不太好，如果连续两次都是跳跃，而且两次跳跃的距离都至少是 $p$，则蓝跳跳会摔倒，这是小蓝不愿意看到的。

  小蓝接到一个特别的任务，要在一个长为 $L$ 舞台上展示蓝跳跳。小蓝要控制蓝跳跳从舞台的左边走到右边，然后掉头，然后从右边走到左边，然后掉头，然后再从左边走到右边，然后掉头，再从右边走到左边，然后掉头，如此往复。

  为了让观者不至于太无趣，小蓝决定让蓝跳跳每次用不同的方式来走。小蓝将蓝跳跳每一步跳的距离记录下来，按顺序排成一列，显然这一列数每个都不超过 $k$ 且和是 $L$。这样走一趟就会出来一列数。如果两列数的长度不同，或者两列数中存在一个位置数值不同，就认为是不同的方案。

  请问蓝跳跳在不摔倒的前提下，有多少种不同的方案从舞台一边走到另一边。

【输入格式】

  输入一行包含三个整数 $k,p,L$。

【输出格式】

  输出一个整数，表示答案。答案可能很大，请输出答案除以 $20201114$ 的余数。

【样例输入 1】

3 2 5

【样例输出 1】

9

【样例输入 2】

5 3 10

【样例输出 2】

397

【样例说明】
  对于样例输入 1，蓝跳跳有以下 9 种跳法：
 1. 1+1+1+1+1
 2. 1+1+1+2
 3. 1+1+2+1
 4. 1+2+1+1
 5. 2+1+1+1
 6. 2+1+2
 7. 1+1+3
 8. 1+3+1
 9. 3+1+1

【评测用例规模与约定】

  对于 $30\%$ 的评测用例，$1\le p\le k\le 50,1\le L\le 1000$。
  对于 $60\%$ 的评测用例，$1\le p\le k\le 50,1\le L\le 10^9$。
  对于 $80\%$ 的评测用例，$1\le p\le k\le 200,1\le L\le 10^{18}$。
  对于所有评测用例，$1\le p\le k\le 1000,1\le L\le 10^{18}$。

---

不会

---

  又对着这题自闭一下午。

转载自CSDN-专业IT技术社区

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/qq_43449564/article/details/124584232